Rによるカーネル密度推定
カーネル密度推定は,各観測点に対して得られたスパースなデータ (密度) を用いて,未だ観測されていない点におけるデータ (密度) を推測するための手法である.統計学においてカーネルという言葉は数個の別の意味で使われる場合がある.そのひとつとしてカーネルを重み付け関数の意味で使うが,このカーネル密度推定のカーネルはそれを指す.
二次元カーネル密度推定
コマンド kde2d() を用いることで二次元カーネル密度推定が可能である.二次元カーネル密度推定で扱うデータは2次元ではなく,3次元データとなる.以下の csv データにあるように,A から Q の17点で何らかの観測値 s が得られた場合のカーネル密度推定を行う.
,x,y,s A,1,4,3 B,2,14,2 C,2,2,1 D,2,8,1 E,2,12,1 F,3,7,3 G,4,4,2 H,11,22,1 I,13,3,2 J,15,19,2 K,15,13,1 L,16,14,1 M,16,5,2 N,18,23,4 O,21,3,3 P,22,7,5 Q,24,15,3
最初にこのデータをコピーした後に以下のコマンドを打つことで読み込む.
$ dd=read.table("clipboard",sep=",",row.names=1,header=T)
次に,データを整形する.kde2d() の入力データは2次元である必要があるので,A の (1,4) を3個 (s個),B の (2,14) を2個,...,Q の (24,15) を3個複製し,それぞれの x座標と y座標をベクトル変数 vx と vy に格納する.以下のコマンドで実行できる.
$ vx=c()
$ vy=c()
$ for(i in 1:17)
+ {
+ for(j in 1:dd[i,3])
+ {
+ vx=c(vx,dd[i,1])
+ vy=c(vy,dd[i,2])
+ }
+ }
このように得たデータをXY平面上にプロットしてみる.この操作はカーネル密度推定には直接は関係ない.
$ plot(vx,vy)
これを実行した結果は以下のようになる.点が集中している領域が,観測値 s が大きいところである.

二次元カーネル密度推定はパッケージ MASS によって行うことができる.以下のようにパッケージをインストールして,ライブラリを読み込む.このとき,既にパッケージをインストールしている場合は1行目は不要.
$ install.packages("MASS", repos="http://cran.ism.ac.jp/")
$ library(MASS)
コマンド kde2d() は以下のように使う.x および y にはそれぞれ x と y の座標. h にはカーネル密度の推定をする際の各々の軸に対するバンド幅を決定するベクトルを指定.バンド幅は,自身のデータに合わせて一番良い結果が得られるように適当な値を見つけ出す.これを決定する際の目安にはバンド幅決定関数を用いる.ここでは bandwidth.nrd を使用する.n はカーネル密度推定をする際に,どれだけのグリッドを発生させるかを示す.この値を大きくすると結果として得られる座標がよりきめ細かになる.lims は c(xi, xj, yi, yj) のように指定することで各座標軸で密度推定をする範囲を指定する.c(-12,0,-14,4) のように指定すると x軸の密度推定は-12から0,y軸の密度推定は-14から0の範囲でのみ行われる.基本的には指定しなくて良い.
kde2d(x, y, h, n, lims = c(range(x), range(y)))
実際には以下のように打つ.これを実行した結果,オブジェクト rd の $xに密度計算後のx座標,$y に密度計算後のx座標,$z にその座標に対応するの密度が格納される.
$ rd=kde2d(x=vx,y=vy,h=c(bandwidth.nrd(vx),bandwidth.nrd(vy)),n=50)
次に得られた結果を以下のコマンドで画像化する.
$ image(x=rd,xlab="vx",ylab="vy")
これを実行した結果は以下のようになる.白く光っている領域が値 s が大きい部分となる.

また,以下のコマンドを打つと等高線を描くことができる.
$ contour(x=rd,xlab="vx",ylab="vy")
これを実行した結果は以下のようになる.

バンド幅を決定する関数には以下のようなものがある.
| コマンド | パッケージ |
|---|---|
| bandwidth.nrd() | MASS |
| ucv() | MASS |
| bcv() | MASS |
| width.SJ() | MASS |
| bw.nrd0() | stats |
| bw.nrd() | stats |
| bw.ucv() | stats |
| bw.bcv() | stats |
| bw.SJ() | stats |
三次元カーネル密度推定
三次元カーネル密度推定では以下のような4次元データを扱える.以下のデータは x,y,z それぞれが0から3の座標を持ち,合計64の各観測点には値 s が収められている.
,x,y,z,s g000,0,0,0,42 g001,0,0,1,33 g002,0,0,2,29 g003,0,0,3,10 g010,0,1,0,46 g011,0,1,1,37 g012,0,1,2,33 g013,0,1,3,26 g020,0,2,0,65 g021,0,2,1,47 g022,0,2,2,49 g023,0,2,3,36 g030,0,3,0,77 g031,0,3,1,64 g032,0,3,2,53 g033,0,3,3,46 g100,1,0,0,52 g101,1,0,1,51 g102,1,0,2,38 g103,1,0,3,19 g110,1,1,0,66 g111,1,1,1,54 g112,1,1,2,47 g113,1,1,3,26 g120,1,2,0,80 g121,1,2,1,66 g122,1,2,2,56 g123,1,2,3,49 g130,1,3,0,80 g131,1,3,1,82 g132,1,3,2,62 g133,1,3,3,49 g200,2,0,0,63 g201,2,0,1,55 g202,2,0,2,45 g203,2,0,3,28 g210,2,1,0,75 g211,2,1,1,69 g212,2,1,2,59 g213,2,1,3,37 g220,2,2,0,85 g221,2,2,1,79 g222,2,2,2,77 g223,2,2,3,57 g230,2,3,0,93 g231,2,3,1,84 g232,2,3,2,69 g233,2,3,3,67 g300,3,0,0,53 g301,3,0,1,41 g302,3,0,2,34 g303,3,0,3,20 g310,3,1,0,62 g311,3,1,1,49 g312,3,1,2,47 g313,3,1,3,32 g320,3,2,0,65 g321,3,2,1,56 g322,3,2,2,58 g323,3,2,3,43 g330,3,3,0,79 g331,3,3,1,74 g332,3,3,2,64 g333,3,3,3,58
このデータを以下のコマンドで読み込む.ここで,data.txt はファイル名.
$ dd=read.table("data.txt",sep=",",row.names=1,header=T)
次にデータを整形する.二次元カーネル密度で行なったのと同様に各データ点をs個分複製して,それの各座標の値をそれぞれ,ベクトル変数 vx,vy,vz に格納する.
$ vx=c()
$ vy=c()
$ vz=c()
$ for(i in 1:64)
+ {
+ for(j in 1:dd[i,4])
+ {
+ vx=c(vx,dd[i,1])
+ vy=c(vy,dd[i,2])
+ vz=c(vz,dd[i,3])
+ }
+ }
次にライブラリを読み込む.インストールしていない場合は install.packages() でインストールする.
$ library(misc3d) $ library(MASS) $ library(rgl)
以上のデータに対してカーネル密度推定は以下のコマンド行なう.コマンド kde3d() の使い方は上の kde2d() と同様で次元数が1個増えるだけ.
$ rd=kde3d(x=vx,y=vy,z=vz,h=c(bandwidth.nrd(vx),bandwidth.nrd(vy),bandwidth.nrd(vz)),n=50)
得られた結果を図示するには以下のコマンドを打つ.
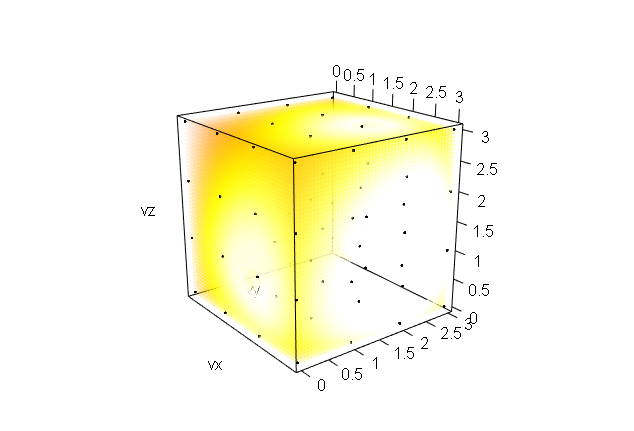
plot3d(x=vx,y=vy,z=vz) image3d(v=rd$d,x=rd$x,y=rd$y,z=rd$z,add=T,vlim=c(0,0.011))
これを実行した結果は以下のようになる.密度が高いところは色が濃く見える.